We process personal information and data on users of our website, through the use of cookies and other technologies, to deliver our services, personalize advertising, and to analyze website activity. We may share certain information on our users with our advertising and analytics partners. For additional details, please refer to our Privacy Policy.
By clicking “AGREE” below, you agree to our Terms of Use and Privacy Policy , as well as our personal data processing and cookie practices as described therein. You also consent to the transfer of your data to our servers in the United States, where data protection laws may be different from those in your country.
Theory
Network theory methods of complex systems analysis
Near-criticality, universality, scaling
Critical phenomena are closely connected with the phase transitions of a system from one state to another. For instance, gas-liquid transition or non-magnetic-magnetic transition.
These transitions can be caused by external forces (like an external magnetic field) or by intrinsic interaction between degrees of freedom in a system. Generally, such transitions associated with a certain parameter, which differs markedly in different phases of a system (for instance, this parameter can be equal to zero in one phase and be non-zero in another phase). The value of the parameter when the transition occurs is called critical point.
Behavior of a system in the vicinity of critical point is called critical behavior. Such behavior can be described in term of a few parameters, which are called critical indices. The validity of this statement is provided by the concepts of modern theoretical physics like scaling and universality.
These transitions can be caused by external forces (like an external magnetic field) or by intrinsic interaction between degrees of freedom in a system. Generally, such transitions associated with a certain parameter, which differs markedly in different phases of a system (for instance, this parameter can be equal to zero in one phase and be non-zero in another phase). The value of the parameter when the transition occurs is called critical point.
Behavior of a system in the vicinity of critical point is called critical behavior. Such behavior can be described in term of a few parameters, which are called critical indices. The validity of this statement is provided by the concepts of modern theoretical physics like scaling and universality.
Scaling, or more precisely, scaling invariance is the property of a system near critical point to be invariant under a specific transformation of the system parameters.
Universality in theoretical physics means that in the vicinity of a critical point all the system properties (for instance, thermodynamic properties) exhibit universal behavior: all of them demonstrate power-like dependence with a certain exponent. Each system property has its own exponent. These exponents are called critical indices (or critical exponents). The set of critical indices completely describes behavior of the system near the critical point.
All the model and complicated theories fall into universality classes. Belonging to a given universality class depends on a system properties like a dimensionality of the system, symmetries of the system and etc. All the systems in a given universality class have identical critical indices.
Suppose that it is possible to determine a full set of critical indices for the considered model. It means that all the other problems that associated with the universality class induced by the considered model will be solved.
A number of universality classes is big but it is obvious that a number of different systems exhibiting phase transitions is much bigger.
Due to scaling invariance and universality, two microscopically different systems (for instance, a non-magnetic material and a liquid differ drastically on microscopic scale) can behave identically near the critical point (of course, this point is different for each system). This identical behavior means that all the critical indices coincide.
Universality in theoretical physics means that in the vicinity of a critical point all the system properties (for instance, thermodynamic properties) exhibit universal behavior: all of them demonstrate power-like dependence with a certain exponent. Each system property has its own exponent. These exponents are called critical indices (or critical exponents). The set of critical indices completely describes behavior of the system near the critical point.
All the model and complicated theories fall into universality classes. Belonging to a given universality class depends on a system properties like a dimensionality of the system, symmetries of the system and etc. All the systems in a given universality class have identical critical indices.
Suppose that it is possible to determine a full set of critical indices for the considered model. It means that all the other problems that associated with the universality class induced by the considered model will be solved.
A number of universality classes is big but it is obvious that a number of different systems exhibiting phase transitions is much bigger.
Due to scaling invariance and universality, two microscopically different systems (for instance, a non-magnetic material and a liquid differ drastically on microscopic scale) can behave identically near the critical point (of course, this point is different for each system). This identical behavior means that all the critical indices coincide.









For the gene-regulatory network and some other systems of the organism with internal interaction (for example, blood parameters, network of neurons), a number of publications demonstrate near-critical behavior.
Phase transition in networks means the "order-disorder" transition (when the network loses its structure and becomes random, chaotic). For the example of a gene-regulatory network, this means that the system is quite "flexible" to external fluctuations, but at the same time retains its structure.
Phase transition in networks means the "order-disorder" transition (when the network loses its structure and becomes random, chaotic). For the example of a gene-regulatory network, this means that the system is quite "flexible" to external fluctuations, but at the same time retains its structure.
An example of a network transition from regular to chaotic for the Watts-Strogatz model. In this system, parameter p, the probability of creating an edge, determines the measure of order.
Using observations about universal behavior and near-criticality, one can speculate about the definition of a biomarker of aging and ways to count it.
The properties of universality and near-criticality suggest that there is a group of several quantities that determines the evolution of the network over time. These quantities can be biomarkers of aging. Network structure analysis would permit to find the mentioned values and identify their critical indices. This will give an idea of the biomarkers of aging and answer the question about their number. Perhaps the degree of aging of the human body cannot be determined by only one parameter, and there are several independent parameters.
On the other hand, the critical indices of the gene regulatory network themselves may be associated with biomarkers of aging. During the aging process, critical indices can also evolve over time. Moreover, the scaling links critical indices to each other and demonstrates that these parameters are not independent. Therefore, calculation and deep analyzis of the evolution of a few (strictly speaking, at least three) critical indices would provide the information about the rest.
All the arguments are present in the following scheme:
The properties of universality and near-criticality suggest that there is a group of several quantities that determines the evolution of the network over time. These quantities can be biomarkers of aging. Network structure analysis would permit to find the mentioned values and identify their critical indices. This will give an idea of the biomarkers of aging and answer the question about their number. Perhaps the degree of aging of the human body cannot be determined by only one parameter, and there are several independent parameters.
On the other hand, the critical indices of the gene regulatory network themselves may be associated with biomarkers of aging. During the aging process, critical indices can also evolve over time. Moreover, the scaling links critical indices to each other and demonstrates that these parameters are not independent. Therefore, calculation and deep analyzis of the evolution of a few (strictly speaking, at least three) critical indices would provide the information about the rest.
All the arguments are present in the following scheme:
In addition to near-criticality, recent studies show that microscopically different systems of an organism – networks of interacting methylation sites, blood parameters, transcriptomes – exhibit common properties, and have similar dynamics near the critical point. So, there is a strong evidence that microscopically different regulatory networks of the body belong to one universality class.

Valverde, Sergi, et al. "Structural determinants of criticality in biological networks." Frontiers in physiology 6 (2015): 127.
Kim, Hyobin, and Hiroki Sayama. "How criticality of gene regulatory networks affects the resulting morphogenesis under genetic perturbations." Artificial Life 24.02 (2018): 85-105.
Balleza, Enrique, et al. "Critical dynamics in genetic regulatory networks: examples from four kingdoms." PLoS One 3.6 (2008): e2456.
Kim, Hyobin, and Hiroki Sayama. "The role of criticality of gene regulatory networks in morphogenesis." IEEE Transactions on Cognitive and Developmental Systems 12.3 (2018): 390-400.
Kim, Hyobin, and Hiroki Sayama. "How criticality of gene regulatory networks affects the resulting morphogenesis under genetic perturbations." Artificial Life 24.02 (2018): 85-105.
Balleza, Enrique, et al. "Critical dynamics in genetic regulatory networks: examples from four kingdoms." PLoS One 3.6 (2008): e2456.
Kim, Hyobin, and Hiroki Sayama. "The role of criticality of gene regulatory networks in morphogenesis." IEEE Transactions on Cognitive and Developmental Systems 12.3 (2018): 390-400.
Podolskiy, Dmitriy, et al. "Critical dynamics of gene networks is a mechanism behind aging and Gompertz law." arXiv preprint arXiv:1502.04307 (2015).
Tarkhov, Andrei E., Kirill A. Denisov, and Peter O. Fedichev. "Aging clocks, entropy, and the limits of age-reversal." bioRxiv (2022).
Avchaciov, Konstantin, et al. "Identification of a blood test-based biomarker of aging through deep learning of aging trajectories in large phenotypic datasets of mice." bioRxiv (2020).
Tarkhov, Andrei E., Kirill A. Denisov, and Peter O. Fedichev. "Aging clocks, entropy, and the limits of age-reversal." bioRxiv (2022).
Avchaciov, Konstantin, et al. "Identification of a blood test-based biomarker of aging through deep learning of aging trajectories in large phenotypic datasets of mice." bioRxiv (2020).
Renormalization group

One of the most developed methods for describing critical behavior and investigating critical points of systems from different fields of physics is the renormalization group (RN approach).
RN approach has proven its efficiency for the analysis of complex systems with nonlinearities and a large number of degrees of freedom.
This approach is very developed, well supported mathematically, and can be adapted for application to a specific system.
Among the successful examples of the renormalization group application are the description of superconductivity, topological phase transitions, as well as phase transitions in various polymers.
The renormalization group method is useful when some basic information about the system (for example, the symmetries, the structure of interactions, strict definition of the measure of order) has already been obtained.
To get basic information about the system, it is necessary to apply the classical methods of network research at first.
RN approach has proven its efficiency for the analysis of complex systems with nonlinearities and a large number of degrees of freedom.
This approach is very developed, well supported mathematically, and can be adapted for application to a specific system.
Among the successful examples of the renormalization group application are the description of superconductivity, topological phase transitions, as well as phase transitions in various polymers.
The renormalization group method is useful when some basic information about the system (for example, the symmetries, the structure of interactions, strict definition of the measure of order) has already been obtained.
To get basic information about the system, it is necessary to apply the classical methods of network research at first.
Modern methods of network study


Most of the information about the properties of the network can be obtained from the analysis of its topology (structure). The network topology is determined by the adjacency matrix and its properties.
Spectral properties





Also, by measuring the response of the gene regulatory network spectrum to drugs (external perturbations) and to gene therapy (internal perturbations), it is possible to investigate the effect of therapies or combinations of therapies. Thus, learn to theoretically predict new combinations of therapies that have a synergistic effect.
Spectral properties describe metastable and unstable states of a dynamical system. An ambitious goal is to identify groups of genes that affect the spectrum of the gene regulatory network and change the parameters of quasi-stable states.
Analysis of the spectrum (eigenvalues and vectors) of the adjacency matrix (and related matrices such as the Laplacian of the network) is the starting point of any study.
Below is a network of human diseases (open data) and the eigenvalues of its adjacency matrix (the vertical axis is the eigenvalue itself, the horizontal axis is the eigenvalue number).
Below is a network of human diseases (open data) and the eigenvalues of its adjacency matrix (the vertical axis is the eigenvalue itself, the horizontal axis is the eigenvalue number).

Connectomes spectra studies
Spectral analysis was successfully used for connectome studies and it produced several outstanding results:
It was shown that the human connectome operates near criticality, and properties of this network can be captured by the quite simple mathematical model (Kuramoto model).
The comparative analysis, based on structural connectomes for several organisms - C. elegans, macaque, and human, has demonstrated that the human connectome differs from the other connectomes. This difference can be described quantitatively by graph spectra.
Complicated dynamics of connectome can be described in terms of relatively simple models whose predictions can be experimentally verified.
Network operation mode



Network topology analysis involves various methods. The parameters that answer the question about the regime in which the network is operating (ordered or chaotic) include:
Level spacing distribution – is the distribution of distances between the eigenvalues of the adjacency matrix. This metric is very sensitive to the symmetries of the system and requires preprocessing of the network, which is called unfolding.
Opposite to level spacing distribution, IPR and R-statistics do not require such preprocessing.
Network analysis methods that use various clustering metrics are also widely used. Evaluation of network clustering also helps to understand in which mode the network operates.
>>level spacing distribution
>>inverse participation ratio (IPR)
>>R-statistics
>>inverse participation ratio (IPR)
>>R-statistics
Level spacing distribution – is the distribution of distances between the eigenvalues of the adjacency matrix. This metric is very sensitive to the symmetries of the system and requires preprocessing of the network, which is called unfolding.
Opposite to level spacing distribution, IPR and R-statistics do not require such preprocessing.
Network analysis methods that use various clustering metrics are also widely used. Evaluation of network clustering also helps to understand in which mode the network operates.
The graph shows the dependence of GCS (global clustering coefficient — an "integral" measure of network clustering) from p (probability of connection) for the Watts-Strogatz model.
Small values of p correspond to almost regular graph, large ones — to "chaotic", random.
Small values of p correspond to almost regular graph, large ones — to "chaotic", random.
Example of clustering changes depending on the probability of connection for the Watts-Strogatz model.
Conservation laws
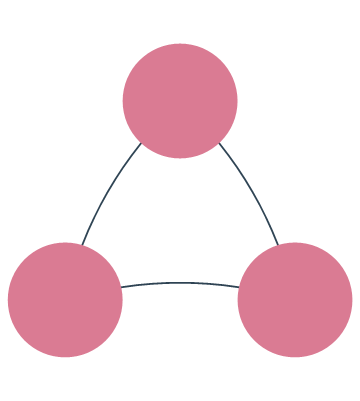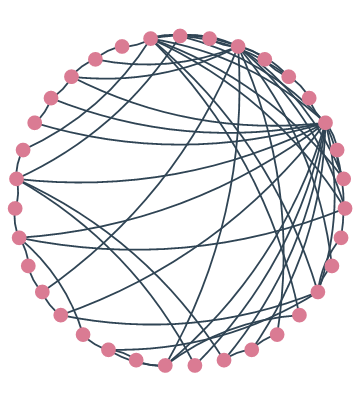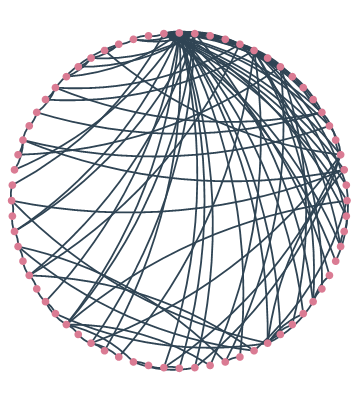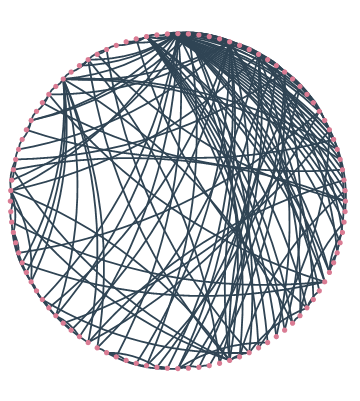


Analysis of network topology and its evolution over time can reveal conservation laws. This approach was used to analyze the connectome. Conservation laws mean the presence of such patterns (motives) in the network as, for example, cliques.
There is a huge variation in life expectancy among different types of organisms. There are incredible examples, such as the arctic sea sponge (Anoxycalyx joubini), an organism from the animal kingdom that is capable of living 15,000 years. The peculiarity of the sponge is the absence of actual tissues and organs; different functions in its organism are performed by various individual cells and cellular layers. Perhaps such a huge lifespan of a sponge is due to the specific conservation laws or invariants of its gene-regulatory network. The search for such invariants will allow us to draw the most important conclusions about the factors determining aging.

A clique is a is a subset of vertices of the network that is a complete graph.
The evolution of networks is an actively studied area today. For example, in studies of network changes over time, click percolation and preferred connection are investigated.
A number of models describes different dynamics of the network topology, such as the Watts-Strogatz algorithm and Barabasi-Albert.
A number of models describes different dynamics of the network topology, such as the Watts-Strogatz algorithm and Barabasi-Albert.
An example of preferential attachment process in the evolution of a network in the Barabashi-Albert model. Connections are formed with bigger probability between vertices with a higher valence.

